Výukový program Decibel: dB a dBm vs. Gain a Milliwatts

Pojem decibel (dB) je pochopitelně obtížný a matoucí pro někoho, kdo se mu právě dostává. Kombinace specifikací pro zisk, výkon a napětí (a proud, ale ne tak často), které mísí dB, dBm, dBW, watty, miliwatty, napětí, milivolty atd., Často vyžaduje převod tam a zpět mezi lineárními hodnotami a hodnotami decibelů. Tento stručný návod pomůže objasnit rozdíl mezi prací s decibelem a prací s lineárními hodnotami.

Logaritmy (logy) byly poprvé koncipovány v časných 1600ech skotským matematikem Johnem Napierem jako nástroj pro zjednodušení operací násobení a dělení jejich převedením na rychlejší a méně závislé operace sčítání a odčítání. To je možné díky způsobu, jak lze násobení dvou čísel vyjádřených jako podobná základní čísla s exponenty dosáhnout pouhým sčítáním exponentů dohromady. Rozdělení stejných čísel se provádí odečtením exponentů. Je to jeden ze zákonů exponentů a vypadá takto:

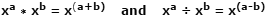
Jako příklad použijeme skutečná čísla, kde x = 10, a = 4, b = 1:

Zákon exponentů funguje pro jakékoli základní číslo, nejen pro 10. Vtip:

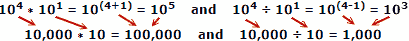
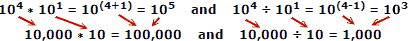
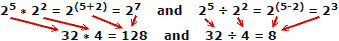
Lidé mají tendenci dělat méně chyb při sčítání a odečítání čísel, takže výhoda logaritmů je zřejmá. Nezapomeňte, že logaritmy byly vyvinuty dříve, než byly k dispozici automatické mechanické nebo elektronické počítače. Pravidlo snímku využívá pro výpočet vlastnosti logaritmů, ale to je samostatné hlavní téma.

Jsou to jednoduché příklady, ale platí pro jakoukoli základnu nebo exponentu. V nepřítomnosti kalkulačky, aby bylo užitečné pro všeobecné použití, potřebujete tabulku čísel a jejich ekvivalentní logaritmy. Počáteční logovací tabulky vyplňovaly svazky v závislosti na mezerách mezi čísly (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3 atd.). Dobrou zprávou pro tvůrce logaritmických tabulek je, že je vyžadována pouze jediná „dekáda“ čísel (např. 1 až 10), protože každá předchozí nebo secesující dekáda je jednoduchým násobkem síly 10u.

Poznámka: V této diskusi používám základní 10, protože to je základ našeho společného číselného systému - odtud termín „společný logaritmus“ pro základní protokoly 10. Možná jste slyšeli o přirozených logaritmech, které používají základ e, ale e se nepoužívá příliš často při výpočtu skalárního elektrického výkonu, napětí a proudových veličin (i když se používá, když jsou zahrnuty fázové úhly, tj. Eulerova identita). Přirozené logaritmy jsou psány jako ln (x) bez indexu 'e', ​​zatímco základní logaritmy 10 jsou obvykle psány jednoduše jako log (x) bez indexu 10; tj. není loge (x) nebo log10 (x).

Na základnu = 10 log tabulka:

Semilogaritmický grafický papír pro cykly 5 - RF CafeVýjimkou a zvláštním případem je logx (0) = Nedefinováno. Je to tak proto, že není energie, na kterou můžete zvýšit libovolné číslo a získat 0 (nula). Můžete asymptoticky přiblížit k nule, ale nemůžete se dostat k nule. Nikdy nebude na stupnici log zobrazen nulový počet; obvykle běží od nějaké síly 10u k nějaké jiné síle deseti. Příklad protokolu grafu je zobrazen napravo. Má rozsah 5 „cyklů“ nebo „desetiletí“. Všimněte si, že na ose y není nula.

Základní logaritmus čísla 10 čísla je tedy exponentem, na který musí být 10 zvýšen, aby získal toto číslo. Jinými slovy, protože 10 zvýšený na výkon 2 je roven 100 (102 = 100), log 10 základní-100 je 2 (log10 100 = 2).

Toto je základní zákon logaritmů:


Provádění stejných multiplikací a dělení jako v horní části stránky pomocí skutečných logaritmů:



To je v pořádku, ale nakonec skončí logaritmus čísla, které hledáte. Otázka: S výjimkou jednoduchého příkladu, jako je tento, jak získáte odpověď, kterou potřebujete? Odpověď: Podívejte se na antilogaritmus (antilog) výsledku. V tomto případě:

Tvrdší a pravděpodobnější příklad s čísly, která nejsou celočíselnými silami 10, by mohl vypadat asi takto:




 Kalkulačka HP-35 (wikipedia) - RF CafeS logaritmus 'x' se rovná 1.8444, antilog se rovná 'x', což je 69.9



Použil jsem kalkulačku k vyhledání protokolů a antilogů pro tato čísla, ale před 1972, když společnost Hewlett Packard (HP) představila vědeckou kalkulačku HP-35, průměrný člověk bez přístupu k podnikovému nebo univerzálnímu počítači sálového počítače potřeboval použít protokol tabulky k provedení těchto výpočtů.

Kdo se obtěžuje používat logaritmy dnes, můžete se zeptat? Spousta lidí, včetně mě, docela často při výpočtu kaskádových systémových parametrů, jako je šumový obraz (NF) a záchytné body (IP). Jednoduché sčítání a odečítání hodnot zesílení a výkonu dBm nefunguje s NF a IP. Řídící vzorce používají násobení a dělení hodnot lineárního zesílení a výkonu, což vyžaduje nejprve převést dB a / nebo dBm na lineární čísla (poměr zisku a mW) pomocí antilogů, provést kaskádové výpočty a poté převést výsledek zpět na dB a / / nebo dBm pomocí protokolů.

Ne všechny kaskádové operace systému vyžadují převádění tam a zpět. Například, pokud je potřeba pouze celkový systémový zisk a / nebo výstupní výkonová úroveň, pak lze výpočty provádět buď s lineárními jednotkami (mW a multiplikátory) nebo s logaritmickými jednotkami (dBm, respektive dB).

Definice „dB“ a „dBm“

Decibel (dB) v elektrotechnice je definován jako 10 krát logaritmus báze-10 poměru mezi dvěma úrovněmi výkonu; např. Pout / Pin (jinými slovy zisk). Vtip:

Všechny zisky větší než 1 jsou proto vyjádřeny jako kladné decibely (> 0) a zisky menší než 1 jsou vyjádřeny jako záporné decibely (<0). Všimněte si, že v případech, s nimiž se většina z nás setká, musí být lineární poměr P1 / P2 kladné číslo (> 0), protože logaritmus 0 je nedefinovaný a logaritmus záporných čísel je složitý (obsahují reálnou i imaginární část ). Hodnota dB však může teoreticky nabývat jakékoli hodnoty mezi −∞ a + ∞, včetně 0, což je zisk 1 [10 * log (1) = 0 dB].

'dBm' je jednotka výkonu založená na decibelech, která je vztažena na 1 mW. Protože zisk 0 dB se rovná zisku 1, je výkon 1 mW o 0 dB větší než 1 mW nebo 0 dBm. Podobně výkonová jednotka dBW je decibelů vzhledem k 1 W výkonu.


V souladu s tím jsou všechny hodnoty dBm větší než 0 větší než 1 mW a všechny hodnoty dBm menší než 0 jsou menší než 1 mW (viz obr. 1). Například + 3.01 dBm je 3.01 dB větší než 1 mW; tj. nebo 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). - 3.01 dBm je 3.01 dB menší než 1 mW; tj. nebo 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Následující tabulka uvádí několik číselných příkladů, takže můžete vidět korelaci mezi mW a dBm. Stejná sada hodnot vynesených na logaritmické stupnici by vytvořila přímku. Kvůli logaritmickému vztahu seskupí graf menší hodnoty proti levé svislé ose. Zvětšená verze mW oblasti 0 až 1 je jasná.

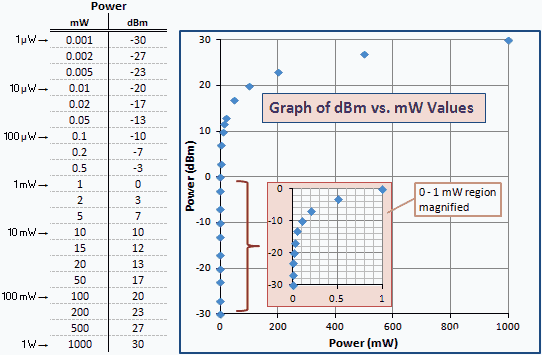
Obr. 1 - graf výkonu v jednotkách dBm vs. mW

Obr. 2 je tabulka a graf poměrů dB vs. lineárního zisku podobné dBm vs. mW na Obr. 1. Všimněte si, že čísla a křivky jsou úplně stejné; změní se pouze popisky os. To proto, že dBm je jednotka výkonu vyjádřená v dB vzhledem k 1 mW (0 dBm).

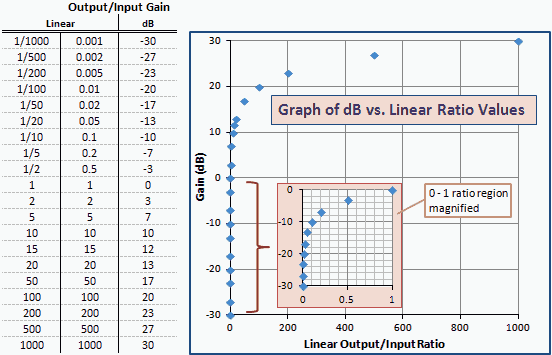
Obr. 2 - graf zisku v jednotkách dBm vs. lineární poměr

Zisk je v zásadě multiplikační (nebo dělící) faktor. Jako příklad může mít zesilovač zesílení, které zvyšuje signál faktorem 4 (tj. 4x) ze vstupu na výstup (viz obr. 3). Pokud je do zesilovače přiváděn signál 1 mW (0 dBm), vyjde 1 mW * 4 = 4 mW. Pokud jde o decibely, faktor 4 je ekvivalentní 10 * log (4) = 6.02 dB, takže 0 dBm v plus 6.02 dB výtěžků + 6.02 dBm na výstupu.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

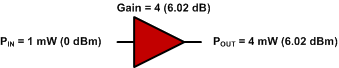
Obr. 3 - Zisk jednoho zesilovače.

Kombinace zisků (lineární a dB) w / kladná hodnota

Pokud je zesilovač se ziskem 4 v sérii s druhým zesilovačem se ziskem 6, pak je celkový zisk 4 * 6 = 24. Z hlediska decibelů je faktor 6 ekvivalentní 10 * log (6) = 7.78 dB a faktor 24 je ekvivalentní 10 * log (24) = 13.8 dB.

Stejně jako 4 x 6 = 24 (lineární zisk), 6.02 dB + 7.78 dB = 13.8 dB (decibel zisk).

Pokud je do zesilovače přiváděn signál 1 mW (0 dBm), pak 4 mW vychází z prvního zesilovače a 24 mW vychází z druhého zesilovače. Viz obr. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Obr. 4 - Kaskádový zisk dvojitého zesilovače.

Kombinace zisku a ztráty (lineární a dB)
Tento další příklad ukazuje, co se stane, když dojde k zesílení <1 (ztráta), kde je za první zesilovač umístěn zeslabovač se ziskem 1/6 namísto druhého zesilovače. Viz obr.
4 * 1 / 6 = 2 / 3 (lineární zisk). Podobně 6.02 dB - 7.78 dB = −1.76 dB (decibel zisk).
Stejně jako v předchozím příkladu, pokud je signál 1 mW (0 dBm) přiveden do zesilovače se ziskem 4, pak 4 mW vyjde. Tento 4 mW poté jde do atenuátoru s lineárním ziskem 1 / 6 a vychází na úrovni výkonu 4 / 6 mW (2 / 3 mW).
Celkový zisk v tomto případě je 4 / 6 = 2 / 3, takže výstupní výkon bude ve skutečnosti menší než vstupní výkon.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Obr. 5 - kaskádový zesilovač zesilovače a zeslabovače.

12 mW + 34 mW + 8 mW + 20 dB

Doplňkové informace o logaritmech
Logaritmy produktů
Vlastnost logaritmů použitých implicitně výše uvádí následující a je základem pro schopnost sčítat a odečítat logaritmické hodnoty namísto násobení jejich lineárních ekvivalentů.

'h * j / k * m / n' může představovat kaskádu komponent, které mají tři zařízení (h, j, m) každé se ziskem> 1 a dvě zařízení (k a n) každé se ziskem <1 (viz Obr.6). Celkový zisk systému lze vypočítat buď vynásobením všech hodnot lineárního zisku dohromady, nebo sečtením všech hodnot zisku decibelů dohromady.

Obr. 6 - Kaskádové komponenty

Logaritmy exponentů
Následující je důležité pro pochopení toho, proč je přírůstek energie z hlediska výkonu 10 * log (Pout / Pin) dB, zatímco zisk z hlediska napětí je 20 * log (Vout / Vin) dB.


což je tak proto, že cf se rovná c násobenému samotnými „f“ krát. Například pokud f = 4:


Zisk na základě výkonu vs. Zisk na základě napětí
Zisk energie je Pout / Pin a zisk napětí je Vout / Vin. Zisk energie založený na poměru výkonu v decibelech je definován jako 10 * log (Pout / Pin). Zisk z hlediska napětí je [(Vout2 / R) / (Vin2 / R)], protože podle Ohmova zákona P = V2 / R. 'R' ve jmenovatelích zruší opuštění Vout2 / Vin2, což se rovná (Vout / Vin) 2, jak je definováno pravidlem exponentů, které říká ac / bc = (a / b) c. Proto:

Důležitá poznámka: Přírůstek napětí, pokud jde o napětí, je 10 * log (Vout / Vin) dB, stejný jako přírůstek výkonu, pokud jde o výkon. Platí rovnice 20 * log (Vout / Vin) dB. To je běžný zmatek.


Žádná operace v matematice není libovolná, a to je důvod, proč je ztráta signálu (zisk <1) zobrazena jako záporná hodnota, a proto je odečtena během kaskádového výpočtu. Je to jednoduchá ukázka, ale stojí za zmínku.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Pokud byste chtěli postavit rozhlasovou stanici, vylepšete svůj FM rádiový vysílač nebo potřebujete jakýkoli jiný FM vybavení, neváhejte nás kontaktovat: [chráněno e-mailem].

Zanechat vzkaz 

Seznam zpráv