Výkon a amplituda: watty, volty a referenční decibely

Úvod
V vysokofrekvenčních aplikacích (ale také v mnoha jiných aplikacích) je velmi běžné řešit velmi velké a velmi malé signály. Například transceiver může vysílat výkon 100 W a přijímat pouze 10 fW (nebo 0.000'000'000'000'01 W). Tyto extrémně odlišné úrovně výkonu mohou sdílet stejné obvody. Tyto hodnoty lze samozřejmě vyjádřit ve wattech pomocí inženýrského zápisu (jak je uvedeno výše) nebo pomocí vědeckého zápisu, jako je 1 · 102 W a 1 · 10 – 14 W, ale je obtížné je vyslovit a pokud je exponent chybně napsán , výsledná chyba bude obrovská.

Dalším způsobem je vzít logaritmus a převést všechny síly v dBm. 100 W se stane + 50 dBm a 10 fW se stanou –110 dBm: tato čísla jsou mnohem snáze zpracovatelná ze srdce a psát. Pak, pokud jsou útlum a zisk různých bloků obvodu vyjádřeny také v dB, lze najít konečný výkon, takže je možné jednoduše přidat vše dohromady namísto násobení, což dále zjednodušuje výpočty.

Ne všichni jsou spokojeni s jednotkami dB, dBm a podobnými (pseudo) jednotkami: není nutné je používat, ale jsou tak široce používány ve strojírenství, kterým je velmi obtížné se jim vyhnout.

Nějaká teorie
Decibely (dB) se používají k vyjádření výkonových poměrů logaritmickým způsobem, takže lze pomocí pohodlných čísel porovnat velmi velké a velmi malé síly. Decibel je bezrozměrná pseudo jednotka, protože je definována poměrem dvou sil. Ale protože decibely jsou tak šikovné, aby se vyjádřila skutečná síla místo pouhého bezrozměrného poměru, velmi často se používají odkazované decibely.

Pokud mluvíme o výkonu, následující rovnice definuje úroveň výkonu P v dB výkonu p ve W vztaženého k výkonu p0:

Faktor 10 je způsoben tím, že decibely jsou „desátou zvony“. Ale nikdy jsem neslyšel o žádném měření provedeném v Bells, používají se pouze decibely.

Nejběžnější jednotkou je dBm (vyslovovat „dBm“), známý také jako dBmW nebo decibel-milliwatt: je to jen úroveň výkonu v dB ve srovnání s referenčním výkonem p0 = 1 mW. Někdy se také používají dBW a vyjadřují poměr výkonu vzhledem k p0 = 1 W, ale nejsou příliš běžné.

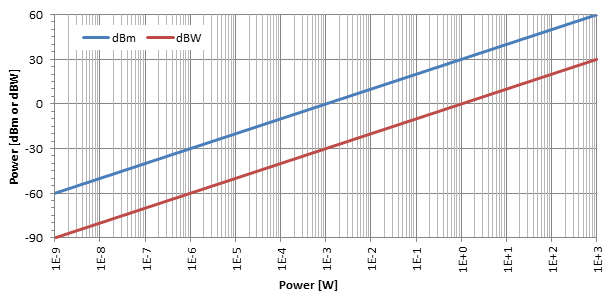
Jak je ukázáno na výše uvedeném grafu, logaritmický účinek konverze decibelů je zcela zřejmý. Jak je vidět na tomto log-line grafu, dBm a dBW jsou pouze dvě přímky oddělené 30 dB: pro převod dBm na dBW jednoduše odečtěte 30.

V některých doménách, jako je příjem analogové televize, je běžné měřit napětí místo energie. To není problém, pokud je impedance známa a pevná (televizní přijímače obvykle používají 75 Ω).

Absolutní napětí může také využít logaritmické stupnice decibel pomocí decibel-mikrovoltů (dBμV) a decibel-voltů (dBV). Nejběžnější je dBμV, které vyjadřují poměr napětí vzhledem k u0 = 1 μV. Někdy se také používají dBV a vyjadřují poměr napětí vzhledem k u0 = 1 V.

Dbejte na to, aby napětí používala ve svém dB vzorci „20“ místo „10“. Je to proto, že decibely jsou vždy definovány jako energetické příděly; pokud máme pouze napětí, musíme je nejprve čtvercovat, abychom našli sílu. Tato síla dvou, když je vyňata z logaritmu, vynásobí existující faktor 10 2.

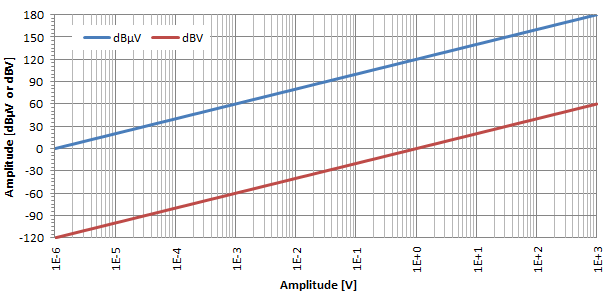
Jak je ukázáno na výše uvedeném grafu a podobným způsobem jako dříve, logaritmický účinek konverze decibelů je zcela evidentní také pro napětí. Jak je vidět na tomto log-line grafu, dBμV a dBV jsou pouze dvě přímky oddělené 120 dB: pro převod dBμV na dBV jednoduše odečtěte 120.

Nyní, pokud chceme převést z energie na napětí a naopak, musíme znát impedanci. Používáme pouze následující rovnici:

Tato konverze je platná, pouze pokud je impedance Zc skutečná a zátěž je přizpůsobena přenosové lince.

Pokud vykreslíme úroveň výkonu v dBm a úroveň amplitudy v dBμV jako funkci výkonu ve W pro danou impedanci (zde Zc = 50 Ω), dostaneme následující:

Stejně jako dříve máme od sebe dvě rovnoběžné čáry 107 dB. Takže pro převod z dBm na dBμV stačí přidat 107 dB pro Zc = 50 Ω, přidat 109 dB pro Zc = 75 Ω, přidat 115 dB pro Zc = 300 Ω nebo přidat 118 dB pro Zc = 600 Ω.

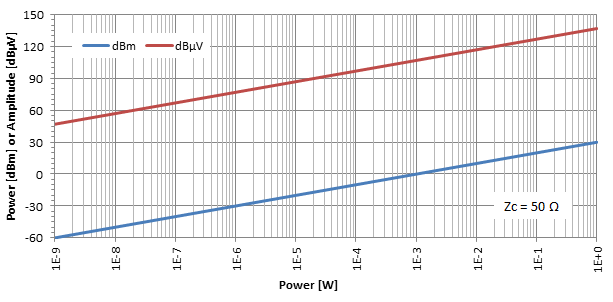
praktické úvahy
Na první pohled si můžeme myslet, že kvůli logaritmu je kapesní kalkulačka naprosto nezbytná k řešení dBm. Ve skutečnosti lze hrubý výpočet snadno provést ve vaší hlavě. Musíte si pamatovat pouze tři fakta:
 Výkon 1 mW je 0 dBm.
 Pokaždé, když se výkon zdvojnásobí, přidejte 3 dB.
 Pokaždé, když se výkon zvýší o faktor 10, přidejte 10 dB.

Nyní se podívejme na několik příkladů: předpokládejme, že máme úroveň výkonu 26 dBm. Můžeme psát 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, a s předchozími třemi simples pravidly, můžeme snadno najít sílu tím, že dělá 1 mW · 10 · 10 · 2 = 2 mW .

Další příklad: předpokládejme, že máme –33dBm: můžeme psát jako –33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB a najdeme 1 mW / 10 / 10 / 10 / 2 μW.

Funguje to také jinak, například 50 mW jsou pouze 1 mW · 10 · 10 / 2. V dBm máme 0 dBm + 10 dB + 10 dB - 3 dB = 17 dBm.

To vyžaduje určitou praxi, ale je to velmi snadné. Není to tak přesné jako kapesní kalkulačka, protože můžete být přesní pouze na ± 2 dB, ale pro úsilí poskytuje velmi dobrou představu o síle signálu.

Podobná metoda funguje také pro dBμV, ale pravidla se liší:
 Amplituda 1 μV je 0 dBμV.
 Pokaždé, když se amplituda zdvojnásobí, přidejte 6 dB.
 Pokaždé, když se amplituda zvýší o faktor 10, přidejte 20 dB.

Možná vás překvapí výše uvedené výpočty v decibelech, kde se dB přidají k dBm, což je docela zvláštní. Je to proto, že decibely jsou pseudo-jednotky a nechovají se jako obvykle. Poměr dvou výkonů je vyjádřen v dB, ale je bezrozměrný: například 3 dB znamená pouze „dvakrát tolik“. Výkon vyjádřený v dBm je skutečně výkon: například 10 dBm znamená „10 krát silnější než 1 mW“, což je 10 mW.

Nyní, když přidáte decibely (dB, dBm, ...), díky jejich logaritmické povaze vynásobíte původní čísla dohromady. Pokud tedy přidáte zisk 3 dB k výkonu 10 dBm, získáte 13 dBm. Ale to, co jste opravdu udělali, znásobuje faktor 2 výkonem 10 mW a získává 20 mW, což je 13 dBm!

Doposud je to dobré, přidávání je mnohem jednodušší, než když se množí, a díky tomu je decibels tak užitečný. Ale je tu problém: protože sčítání decibelů odpovídá násobení původních faktorů, jak lze přidat (kombinovat) sílu dvou signálů? No, nemůžete. K dBm nemůžete přidat dBm. Pokud máte například obvod nebo zařízení, které kombinuje výkon jednoho signálu 10 dBm (10 mW) s výkonem jiného signálu 13 dBm (20 mW), výsledkem je 10 mW + 20 mW = 30 mW, což je 14.8 dBm. Neexistuje žádný způsob, jak to udělat přímo v dBm, musíte převést obě síly ve wattech, sčítat je a převést je zpět v dBm. Toto je velké omezení decibelů a společné úskalí; naštěstí tato operace není příliš běžná.

Pokud byste chtěli postavit rozhlasovou stanici, vylepšete svůj FM rádiový vysílač nebo potřebujete jakýkoli jiný FM vybavení, neváhejte nás kontaktovat: [chráněno e-mailem].

Zanechat vzkaz 

Seznam zpráv